Research about applications 9_RA

In application 13_A we simulated the following random variables

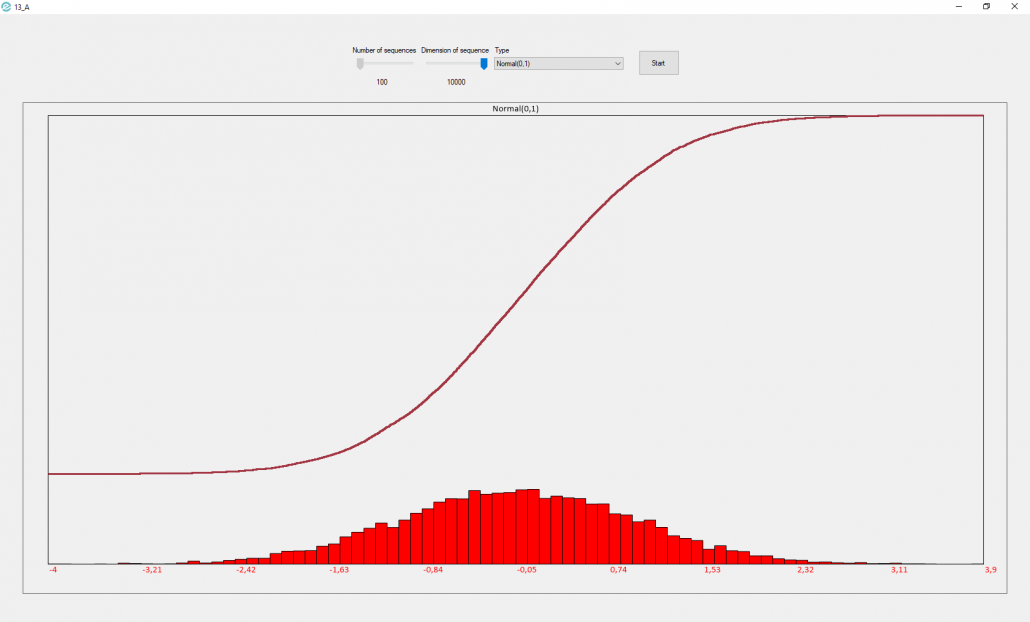
The first image represents the normal distribution with mean 0 and variance 1.

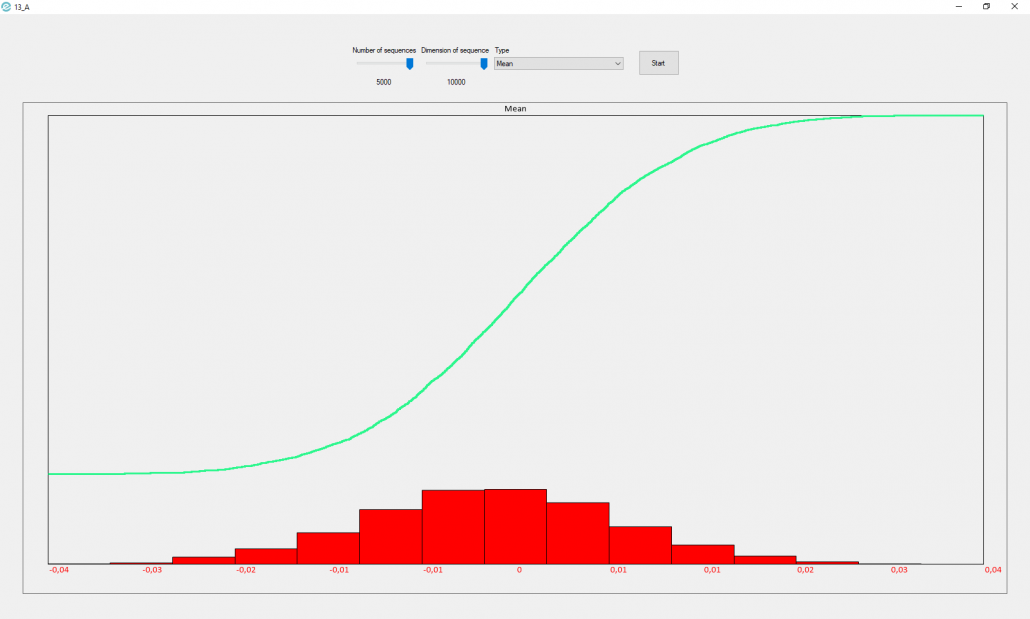
The second image represents the distribution of the mean of m sequences of n numbers generated by a normal with mean 0 and variance 1.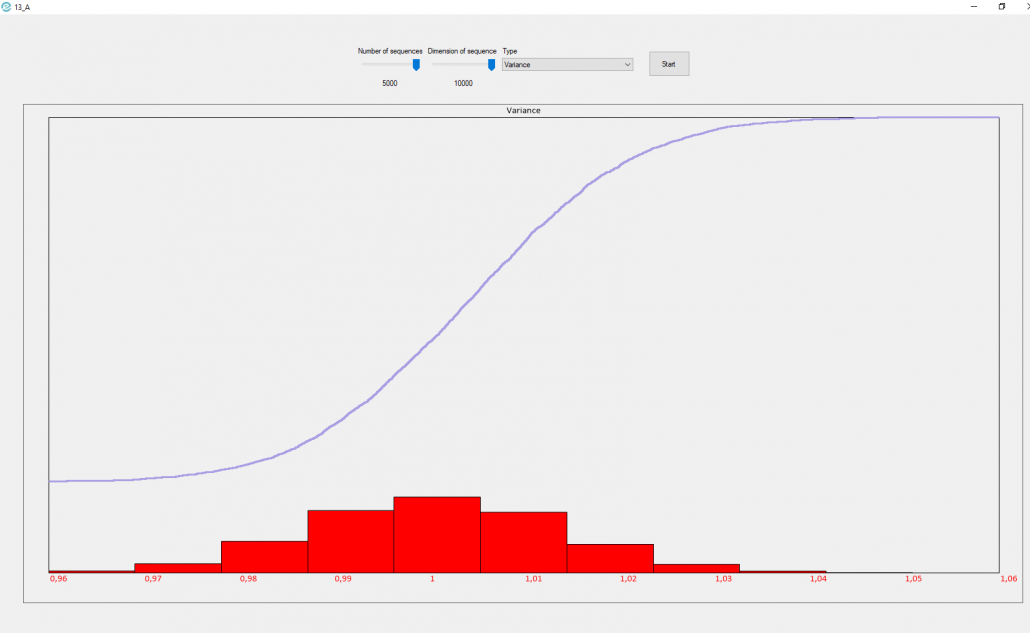

The third image represents the variance distribution of m sequences of n numbers generated from a normal with mean 0 and variance 1.

The fourth image represents the Log-normal distribution with mean $exp \left (\mu+\frac{\sigma^2}{2} \right )$ and variance $\left [ exp\left ( \sigma^2 \right )-1 \right ]exp\left ( 2\mu+\sigma^2 \right )$ .

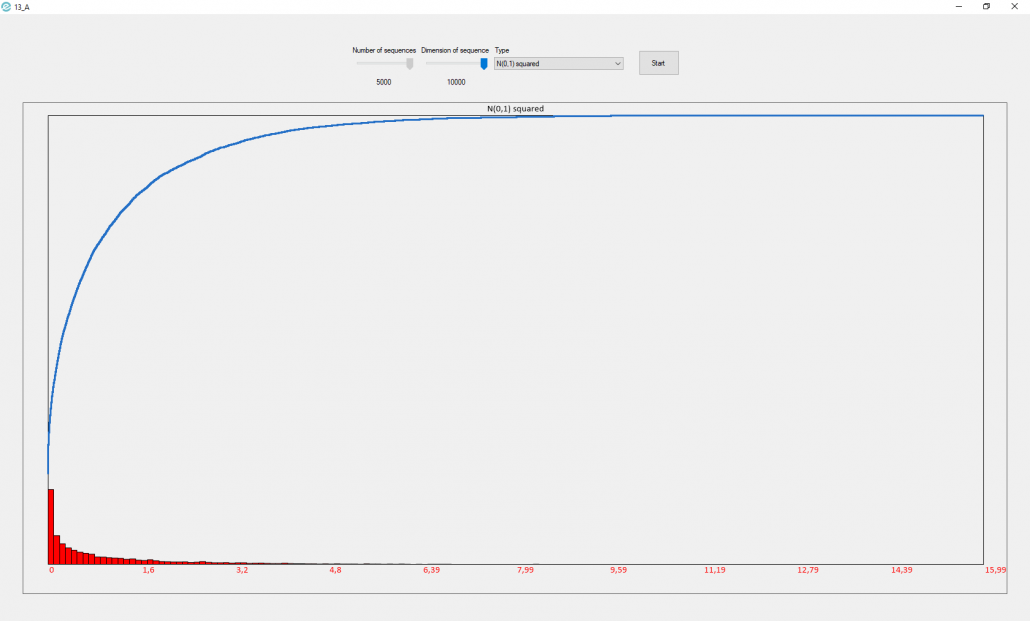
The fifth image represents the Chi-squared distribution with mean is equal to the number of degrees of freedom and variance is equal to two times the number of degrees of freedom.

The sixth image represents the Beta prime distribution with mean $\frac{\alpha}{\beta-1}$ if $\beta> 1$ and variance $\frac{\alpha\left ( \alpha+\beta-1 \right )}{\left ( \beta-2 \right )\left ( \beta-1 \right )^2}$ if $\beta> 2$