Research about theory 13_R

A quick recap about CLT

In probability theory, the central limit theorem (CLT) states that the distribution of a sample variable approximates a normal distribution (i.e., a “bell curve”) as the sample size becomes larger, assuming that all samples are identical in size, and regardless of the population’s actual distribution shape.

Put another way, CLT is a statistical premise that, given a sufficiently large sample size from a population with a finite level of variance, the mean of all sampled variables from the same population will be approximately equal to the mean of the whole population. Furthermore, these samples approximate a normal distribution, with their variances being approximately equal to the variance of the population as the sample size gets larger, according to the law of large numbers.

Introduction to Wiener Process (also called Brownian Motion)

The concept of a Brownian motion was discovered when Einstein observed particles oscillating in liquid. Since fluid dynamics are so chaotic and rapid at the molecular level, this process can be modelled best by assuming the particles move randomly and independently of their past motion. We can also think of Brownian motion as the limit of a random walk as its time and space increments shrink to 0. In addition to its physical importance,
Brownian motion is a central concept in stochastic calculus.

Definition of Wiener Process

A standard (one-dimensional) Wiener process (also called Brownian motion) is a stochastic process $\left \{ W_t \right \}_{t\geq 0}$ indexed by nonnegative real numbers t with the following properties:

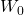$W_0$ = 0.
With probability 1, the function t → Wt is continuous in t.
The process 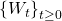$\left \{ W_t \right \}_{t\geq 0}$ has stationary, independent increments.
The increment 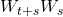$W_{t+s} − W_s$ has the 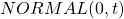$NORMAL(0, t)$ distribution.

Wiener Process as a scaling limit of Random Walks

One of the many reasons that Brownian motion is important in probability theory is that it is, in a certain sense, a limit of rescaled simple random walks. Let $ξ_1, ξ_2, …$ be a sequence of independent, identically distributed random variables with mean 0 and variance 1. For each $n\geq 1$ define a continuous-time stochastic process $\left \{ W_{n(t)} \right \}_{t\geq 0}$ by:

This is a random step function with jumps of size $\pm 1\sqrt{n}$ at times $V$ , where $k\in \mathbb{Z}^+$ . Since the random variables $ξ_j$ are independent, the increments of $W_{n(t)}$ are independent. Moreover, for large n the distribution of $W_n(t + s) − W_n(s)$ is close to the $NORMAL(0, t)$ distribution, by the Central Limit theorem. Thus, it requires only a small leap of faith to believe that, as $n\rightarrow \infty$ , the distribution of the random function $W_n(t)$ approaches (in a sense made precise below) that of a standard Brownian motion.
Why is this important? First, it explains, at least in part, why the Wiener process arises so commonly in nature. Many stochastic processes behave, at least for long stretches of time, like random walks with small but frequent jumps. The argument above suggests that such processes will look, at least approximately, and on the appropriate time scale, like Brownian motion.
Second, it suggests that many important “statistics” of the random walk will have limiting distributions and that the limiting distributions will be the distributions of the corresponding statistics of Brownian motion. The simplest instance of this principle is the central limit theorem: the distribution of $W_n(1)$ is, for large n close to that of $W(1)$ (the gaussian distribution with mean 0 and variance 1). Other important instances do not follow so easily from the central limit theorem. For example, the distribution of:

converges, as $n\rightarrow \infty$ , to that of:

Donsker’s Theorem

In probability theory, Donsker’s theorem (also known as Donsker’s invariance principle, or the functional central limit theorem), named after Monroe D. Donsker, is a functional extension of the central limit theorem.

Let $X_1, X_2, X_3, \ldots$ be a sequence of independent and identically distributed (i.i.d.) random variables with mean 0 and variance 1.

Let $S_n:=\sum_{i=1}^n X_i$ .

The stochastic process $S:=(S_n)_{n\in\N}$ is known as a random walk. Define the diffusively rescaled random walk (partial-sum process) by

W^{(n)}(t) := \frac{S_{\lfloor nt\rfloor}}{\sqrt{n}}, \qquad t\in [0,1].

The central limit theorem asserts that $W^{(n)}(1)$ converges in distribution to a standard Gaussian random variable $W(1)$ as $n\to \infty$ . Donsker’s invariance principle extends this convergence to the whole function $W^{(n)}:=(W^{(n)}(t))_{t\in [0,1]}$ . More precisely, in its modern form, Donsker’s invariance principle states that: As random variables taking values in the Skorokhod space* $\mathcal{D}[0,1]$ , the random function $W^{(n)}$ converges in distribution to a standard Brownian motion $W:=(W(t))_{t\in [0,1]}$ as $n\to \infty$

*The set of all càdlàg functions from E to M is often denoted by D(E; M) (or simply D) and is called Skorokhod space after the Ukrainian mathematician Anatoliy Skorokhod.