Research about theory 12_R

The concept of a Brownian motion was discovered when Einstein observed particles oscillating in liquid. Since fluid dynamics are so chaotic and rapid at the molecular level, this process can be modeled best by assuming the particles move randomly and independently of their past motion. We can also think of Brownian motion as the limit of a random walk as its time and space increments shrink to 0. In addition to its physical importance, Brownian motion is a central concept in stochastic calculus which can be used in finance and economics to model stock prices and interest rates.

What is Brownian motion and why are we interested?

Much of probability theory is devoted to describing the macroscopic picture emerging in random systems defined by a host of microscopic random effects. Brownian motion is the macroscopic picture emerging from a particle moving randomly in d-dimensional space without making very big jumps. On the microscopic level, at any time step, the particle receives a random displacement, caused for example by other particles hitting it or by an external force, so that, if its position at time zero is $S_0$ , its position at time n is given as $S_n=S_0+\sum ^n _{i=1}X_i$ , where the displacements $X_1, X_2, X_3, ...$ are assumed to be independent, identically distributed random variables with values in $\mathbb{R}^d$ . The process $\left \{ S_n:n\geq 0 \right \}$ is a random walk, the displacements represent the microscopic inputs. It turns out that not all the features of the microscopic inputs contribute to the macroscopic picture. Indeed, if they exist, only the mean and covariance of the displacements are shaping the picture. In other words, all random walks whose displacements have the same mean and covariance matrix give rise to the same macroscopic process, and even the assumption that the displacements have to be independent and identically distributed can be substantially relaxed. This effect is called universality, and the macroscopic process is often called a universal object. It is a common approach in probability to study various phenomena through the associated universal objects.

If the jumps of a random walk are sufficiently tame to become negligible in the macroscopic picture, in particular if it has finite mean and variance, any continuous time stochastic process $\left \{ B(t):t\geq 0 \right \}$ describing the macroscopic features of this random walk should have the following properties:

for all times 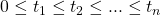$0\leq t_1\leq t_2\leq ...\leq t_n$ the random variables 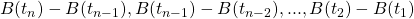$B(t_n)-B(t_{n-1}), B(t_{n-1})-B(t_{n-2}), ..., B(t_2)-B(t_1)$ are independent; we say that the process has independent increments,
the distribution of the increment 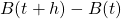$B(t+h)-B(t)$ does not depend on 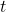$t$ ; we say that the process has stationary increments,
the process 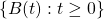$\left \{ B(t):t\geq 0 \right \}$ has almost surely continuous paths.
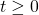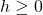for every $t\geq 0$ and $h\geq 0$ the increment 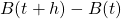$B(t+h)-B(t)$ is multivariate normally distributed with mean 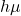$h\mu$ and covariance matrix $h\Sigma \Sigma ^T$ .

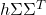Hence any process with the features (1)-(3) above is characterised by just three parameters,

the initial distribution, i.e. the law of $B(0)$ ,
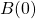the drift vestor $\mu$ ,
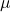the diffusion matrix $\Sigma$ .

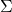If the drift vector is zero, and the diffusion matrix is the identity we say the process is a Brownian motion. If $B(0)=0$ , i.e. the motion is started at the origin, we use the term standard Brownian motion.

Suppose we have a standard Brownian motion $\left \{ B(t):t\geq 0 \right \}$ . If $X$ is a random variable with values in $\mathbb{R}^d$ and $\Sigma$ a $d\times d$ matrix, then it is easy to check that $\left \{ \tilde{B}(t):t\geq 0 \right \}$ given by

$\tilde{B}(t)=X+\mu t+\Sigma B(t)$ , for $t\geq 0$ ,

is a process with the properties (1)-(4) with initial distribution $X$ , drift vestor $\mu$ and diffusion matrix $\Sigma$ . Hence the macroscopic picture emerging from a random walk with finite variance can be fully described by a standard Brownian motion.

References

lecnotes_moerters.pdf (math-berlin.de)

Dahl.pdf (uchicago.edu)

What is Brownian motion and why are we interested?

References

Leave a Reply

Leave a Reply Cancel reply