Researches about theory
8_R.
Do a research about the following topics:
– The law of large numbers LLN, the various definitions of convergence
– The convergence of the Binomial to the normal and Poisson distributions
– The central limit theorem [in anticipation of a topic we will study later]
Applications
8_A. Exercise (also partially described in video 04)
Generate and represent m “sample paths” of n point each (m, n are program parameters), where each point represents a pair of:
time index t, and relative frequency of success f(t),
where f(t) is the sum of t Bernoulli random variables with distribution B(x, p) = p^x(1-p)^(1-x) observed at the various times up to t: j=1, …, t..
At time n (last time) and one other chosen inner time 1
Comment briefly on the result.
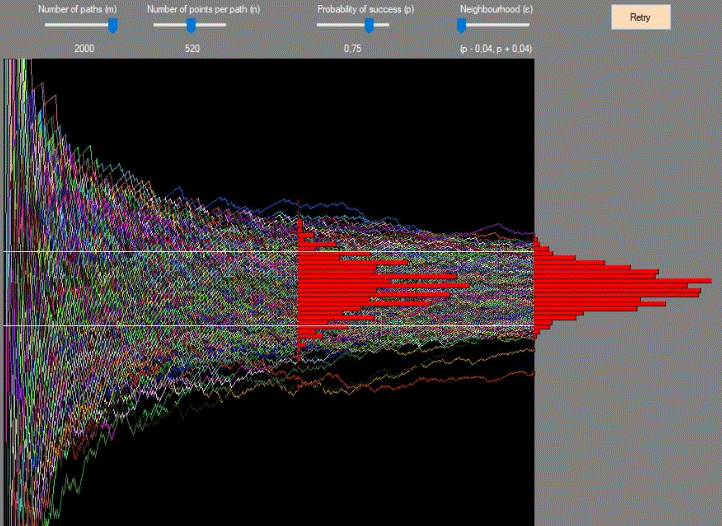(courtesy: homework screenshot by Lorenzo Zara, year 2020)
(The general scheme of this exercise, will also be “reused” in next homeworks where we will consider other more interesting stochastic processes.)
Researches about applications
6_RA. Do a web research about the various methods proposed to compute the running median (one pass, online algorithms).
Store (cite all sources and attributions) the algorithm(s) that you think is(are) a good candidate, explaining briefly how it works and possibly try a quick demo.
Leave a Reply
Want to join the discussion?Feel free to contribute!