Research about theory 6_R

As Kolmogorov said, the probability is an axiom, based on measure theory. The measure is a quantity defined onset, (non-negative, is zero on the empty set, countable additivity).

Given a set X, a power set P(X) (a set of all subsets of all subsets of X), we have a Sigma algebra which is defined as a subset of the power set of x which has some properties.

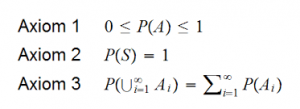
Probability is a particular case of measure with a particular property, it’s defined between a range (0,1), this range is called the Probability Space. The probability space is represented as triples (Ω, a, p) as in the measure space, where the triples are ( X, Σ, μ).

Ω: is a set of all elements, a: is the sigma-algebra on the set X, p is the probability function.

Starting from empirical objects, I can derive an infinite number of models (theoretical models), defined by the Θ parameter (state of nature) and from these, I can calculate the most probable model, thanks to the role that probability has in statistics.

Introduction

Probability and statistics, the branches of mathematics concerned with the laws governing random events, including the collection, analysis, interpretation, and display of numerical data. Probability has its origin in the study of gambling and insurance in the 17th century, and it is now an indispensable tool of both social and natural sciences. Statistics may be said to have its origin in census counts taken thousands of years ago; as a distinct scientific discipline, however, it was developed in the early 19th century as the study of populations, economies, and moral actions and later in that century as the mathematical tool for analyzing such numbers.

The assumptions as to set up the axioms can be summarised as follows:

Let (Ω, F, P) be a measure space with P(E) being the probability of some event E, and P(Ω) = 1.

Then (Ω, F, P) is a probability space, with sample space Ω, event space F and probability measure P.

First axiom

The probability of an event is a non-negative real number:

where F is the event space. It follows that P(E) is always finite, in contrast with more general measure theory. Theories that assign a negative probability to relax the first axiom.

Second axiom

This is the assumption of unit measure: that the probability that at least one of the elementary events in the entire sample space will occur is 1

P(Ω) = 1

Third axiom

This is the assumption of σ-additivity:

Any countable sequence of disjoint sets (synonymous with mutually exclusive events) E₁, E₂, . . . . satisfies

Many important laws are derived from Kolmogorov’s three axioms. For example, the Law of Large Numbers can be deduced from the laws by logical reasoning (Tijms, 2004).

Mathematical Statistics

Mathematical statistics is the application of probability theory, a branch of mathematics, to statistics, as opposed to techniques for collecting statistical data.

Data analysis is divided into:

descriptive statistics – the part of statistics that describes data, i.e. summarises the data and their typical properties.
inferential statistics – the part of statistics that concludes data (using some model for the data): For example, inferential statistics involves selecting a model for the data, checking whether the data fulfil the conditions of a particular model, and quantifying the involved uncertainty (e.g. using confidence intervals).

The Concrete and the Real

When abstract probability theory makes a distinction between the concrete sample ω (also known as a random outcome or trial) and the event A that is realised if ω ∈ A, it does something entirely new: this is essentially a distinction between the concrete and the real. When probability no longer pertains to the random outcome as such, but only to the event, then the probability is separated from randomness. The great foundational gesture of abstract probability theory was to shatter our image of randomness. There is no random generator any longer, and it is no longer a matter of expecting random outcomes. Once it is understood that the random outcome matters only in so far as it is the set-theoretic element of an event, then set theory becomes the foundation of probability theory, and everything relating to expectation and the concrete field of randomness is reduced to the sole measurement of sets. And when we examine the strong law of large numbers, which is what lends tense to the notion of probability and gives us the impression of expecting something to happen with some probability, we realise that measure theory has only been extended to sets of non-denumerable cardinality, and that we now only measure the set of typical (infinite) random sequences, which is of measure 1 and in which no sequence is distinguished in particular.

Our intuitive image of randomness and the random trial is that of drawing balls from an urn; it is that of the materialisation of the random trial, of the manifestation of the concrete; but in the formalism of probability, everything points in the opposite direction, that of the measure of sets alone, that of the infinite and non-constructive limit where, precisely, individual trials are indistinguishable and lose their identity.

In the real world statistics is more used for examples:

Statistics in the Health Industry

Statistics is playing its part in the health industry. It helps the doctor to take and manage the data of their patients. Apart from that WHO is also using statistics to generate their annual report on the healthy populations of the world. Due to statistics, medical science has invented lots of vaccines and anti tode to fight against major diseases.

Education

The beneficial importance of statistics in education is that teachers can be considered to be supportive as researchers during their classrooms to recognize what education technique works on which pupils and know the reason why. They also need to estimate test details to determine whether students are working expectedly, statistically, or not.

Government

The importance of statistics in government is utilized by making judgments about health, populations, education, and much more. It may help the government to check out what education schedule can be beneficial for students. What is the progress report of high school students using that particular curriculum? The government can assemble specific data about the population of the country using a census.

Statistics in Economics

Whenever you are going to study economics, you would also learn statistics. Statistics and Economics are interrelated with each other. It is impossible to separate them. The development of advanced statistics has opened new ways to extensive use of statistics for Economics.

Almost every branch of Economics uses statistics, i.e., consumption, production, distribution, public finance. All these Economic branches use statistics for comparison, presentation, interpretation, and so on.

Income spending problems on and various sections of the people. National wealth production, demand, and supply adjustment, the effect of economic policies. All these indicate the importance of statistics in the field of economics and its various branches. The government uses statistics in economics to calculate its GDP and Per capita Income.